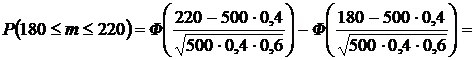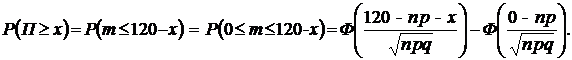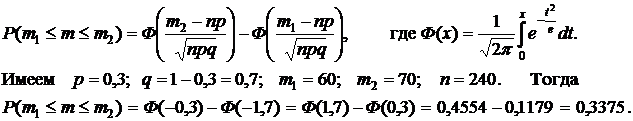Решение. Измеряется скорость ветра в данном пункте Земли
Измеряется скорость ветра в данном пункте Земли. Случайная величина X – проекции вектора скорости ветра на фиксированное направление. Оценить вероятность события , если путем многолетних измерений установлено, что .
За возьмем 80 км/ч и, применив первое неравенство Чебышева, получим => .
21. Предельные теоремы теории вероятностей
Теорема Бернулли. Относительная частота успехов в независимых испытаниях по схеме Бернулли сходятся по вероятности при к вероятности успеха в одном испытании.
Центральная предельная теорема (Ляпунова). Если случайные величины в последовательности независимы, одинаково распределены и имеют конечные математическое ожидание и дисперсию , то для любого действительного
где – стандартизированное среднее арифметическое n случайных величин в последовательности.
Пусть – число успехов в независимых испытаниях по схеме Бернулли. Тогда при достаточно больших значениях
где – табулирована и (интегральная теорема Муавра – Лапласа).
– функция табулирована (локальная теорема Муавра – Лапласа).
Вероятность появления события в каждом из независимых испытаний равна 0,8. Найти вероятность того, что событие наступит 120 раз в 144 испытаниях.
По условию задачи . Воспользуемся локальной теоремой Лапласа. Найдем значение аргумента
По таблице функций находим, что . Искомая вероятность равна
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Глава 5. «Предельные законы теории вероятностей».
Пример 5.1. Дана случайная величина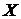 
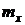
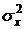
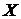
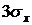
с математическим ожиданием 
и дисперсией 
. Оценить сверху вероятность того, что величина отклонится от своего математического ожидания не меньше, чем на 
.
Решение. Полагая во втором неравенстве Чебышева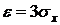 
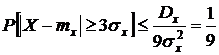
, получим
,
т.е. вероятность того, что отклонение случайной величины от ее математического ожидания выйдет за пределы трех средних квадратических отклонений, не может быть больше 1/9 ни при каком законе распределения.
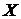
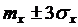
Замечание. На практике в большинстве случаев вероятность того, что величина выйдет за пределы участка 
, значительно меньше 1/9. Например, для нормального закона эта вероятность приблизительно равна 0.003.
Пример 5.2.Среднее значение скорости ветра в данной местности равно 16 км/час. Оценить вероятность того, что в данной местности скорость ветра (при одном наблюдении) не превышает 80 км/час.
Решение.По первой форме неравенства Чебышева находим
.
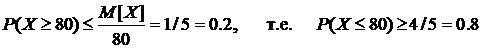
Пример 5.3.Математическое ожидание скорости ветра на данной высоте равно 25 км/час, а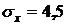 
км/час. Какие скорости ветра можно ожидать на этой высоте с вероятностью не меньшей чем 0.9?
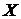
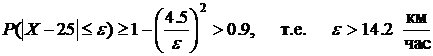
Решение. Пусть — скорость ветра. Тогда по второму неравенству Чебышева имеем 
.
Следовательно, с вероятностью, большей 0.9, имеем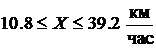 
.
Пример 5.4. 4 станка производят детали из стали марки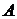 
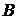
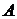
, 6 других – из стали марки 
. Определить вероятность того, что из 500 взятых деталей количество деталей из стали марки будет заключено в пределах от 180 до 220.
Решение. Воспользуемся неравенством Чебышева для оценки нижней границы искомой вероятности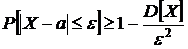 
.
Имеем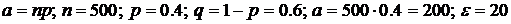 
.
.
.
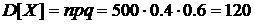
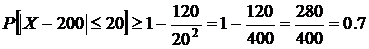
С другой стороны, эту вероятность можно более точно вычислить (оценить) по теореме Муавра–Лапласа:
,
.
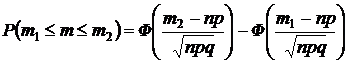
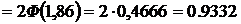
Пример 5.5.Станок–автомат требует подналадки в среднем один раз за 4 часа работы. Определить вероятность того, что за 10 суток непрерывной работы подналадка осуществлялась ровно 70 раз.
Решение.Имеем n = 240; m = 70; p = 0.25; q = 0.75.
По локальной теореме Муавра–Лапласа получаем
.
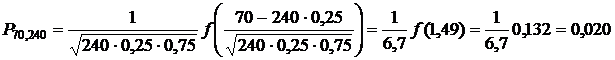
По закону Пуассона эта вероятность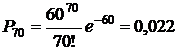 
.
Пример 5.6. В страховой фирме застраховано 10 тысяч лиц одного возраста и одной социальной группы. Вероятность смерти в течение года для каждого лица равна 0,006. Каждый застрахованный в начале года вносит 12 долларов страховых, и, в случае смерти, его родственники получают от фирмы тысячу долларов. Найти вероятность того, что:
2) фирма получит прибыль, не меньшую чем x тысяч долларов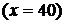 
.
Решение. Вероятность убытков для страховой фирмы есть вероятность смерти в течении года более чем 120 застрахованных.
Тогда по формуле Муавра–Лапласа имеем
.
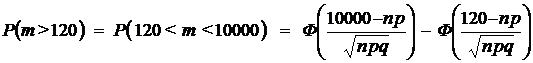
У нас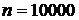 
; 
; 
.
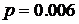
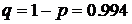
Тогда с точностью до 10 знаков после запятой
.
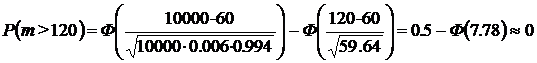
Получение прибыли в xтысяч долларов и более может быть, если в течении года из застрахованных умрёт не более чем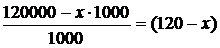 
человек. В этом случае вероятность получения фирмой прибыли (П) не менее величины xравна:
При 
получим: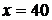
.
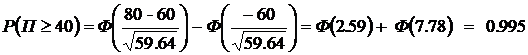
Пример 5.7.Три станка, производительности которых соотносятся как 5:3:2, производят детали на общий конвейер. Определить вероятность того, что из 240 деталей, взятых случайным образом с конвейера, деталей, произведенных вторым станком будет от 60 до 70.
Решение.Искомую вероятность определяем по интегральной формуле Муавра–Лапласа:
Пример 5.8.Вероятность изделию быть бракованным равна 0,05. Сколько изделий надо взять, чтобы с вероятностью не меньшей 0,9 среди них оказалось не менее 50 бракованных?
Решение.Необходимо найти число n, удовлетворяющее интегральной формуле Муавра–Лапласа
P(50 Ј m Ј n) =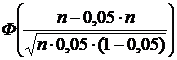 
– 
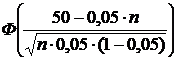
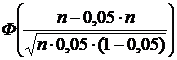
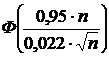
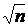
і 0,9 .
= 
» Ф(4,3 
) і Ф(30) » 0,5.
Тогда 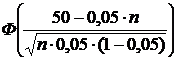Ј – 0,4.
По таблице функции Лапласа находим, что Ф(х) = – 0,4 при х = 1,28.
Поэтому получаем соотношение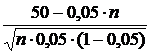 
Ј 1,28
или 0,05Чn – 0,282Ч 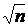– 50 і 0.
Решая последнее неравенство, находим n і 1196, то есть следует взять не менее 1196 изделий.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Источник
Скорость и сила ветра
Ветер – это горизонтальное перемещение (поток воздуха параллельно земной поверхности), возникающее в результате неравномерного распределения тепла и атмосферного давления и направленное из зоны высокого давления в зону низкого давления.
Ветер характеризуется скоростью (силой) и направлением. Направление определяется сторонами горизонта, откуда он дует, и измеряется в градусах. Скорость ветра измеряется в метрах в секунду и километрах в час. Сила ветра измеряется в баллах.
Ветер в ботфортах, м/с, км/час
Шкала Бофорта — условная шкaлa для визуальной оценки и записи силы (скорости) ветра в баллах. Первоначально, была разработана английским адмиралом Френсисом Бофортом в 1806 г. для определения силы ветра по характеру её проявления на море. С 1874 г. данная классификация принята для повсеместного (на суше и на море) использования в международной синоптической практике. В последующие годы менялась и уточнялась (таблица 2). За ноль баллов было принято состояние полного штиля на море. Изначально система была тринадцатибальная (0-12 bft, по шкале Бофорта). В 1946г. шкалу увеличили до семнадцати (0-17). Сила ветра в шкале определяется по взаимодействию ветра с различными предметами. В последние годы, силу ветра, чаще, оценивают по скорости, измеряемой в метрах в секунду — у земной поверхности, на высоте порядка 10м над открытой, ровной поверхностью.
В таблице приведена шкала Бофорта, принятая в 1963 году Всемирной метеорологической организацией.
Сила ветра в баллах по шкале Бофорта
Словесное обозначение силы ветра
Скорость ветра, м/с
Скорость ветра км/ч
Действие ветра
Полное отсутствие ветра. Дым поднимается вертикально, листья деревьев неподвижны.
Дым слегка отклоняется от вертикального направления, листья деревьев неподвижны
Ветер чувствуется лицом, листья временами слабо шелестят, флюгер начинает двигаться,
Листья и тонкие ветки деревьев с листвой непрерывно колеблются, колышутся лёгкие флаги. Дым как бы слизывается с верхушки трубы (при скорости более 4 м/сек).
Ветер поднимает пыль, бумажки. Качаются тонкие ветви деревьев и без листвы. Дым перемешивается в воздухе, теряя форму. Это лучший ветер для работы обычного ветрогенератора (при диаметре ветроколеса 3-6 м)
Качаются ветки и тонкие стволы деревьев, ветер чувствуется рукой. Вытягивает большие флаги. Свистит в ушах.
Качаются толстые сучья деревьев, тонкие деревья гнутся, гудят телеграфные провода, зонтики используются с трудом
Качаются стволы деревьев, гнутся большие ветки, трудно идти против ветра.
Очень
крепкий
Ломаются тонкие и сухие сучья деревьев, говорить на ветру нельзя, идти против ветра очень трудно.
Гнутся большие деревья, ломает большие ветки. Ветер срывает черепицу с крыш
Сильный
шторм
На суше бывает редко. Значительные разрушения строений, ветер валит деревья и вырывает их с корнем
Жестокий
шторм
Наблюдается очень редко. Сопровождается большими разрушениями на значительных пространствах.
Опустошительные разрушения. Отдельные порывы ветра достигают скорости 50—60 м.сек. Ураган может случиться перед сильной грозой
Чтобы легче запомнить
Слабый — 5 м/с (
20 км/час) — листья и тонкие ветки деревьев непрерывно колышутся.
Свежий — 10 м/с (
35 км/час) — вытягивает большие флаги, свистит в ушах.
Крепкий — 15 м/с (
55 км/час) — гудят телеграфные провода, трудно идти против ветра.
Шторм — 25 м/с ( 90 км/час) — ветер валит деревья, разрушает строения.
При возникновении чрезвычайных ситуаций осуществить вызов одной экстренной оперативной службы можно по отдельному номеру любого оператора сотовой связи: это номера 101 (служба пожарной охраны и реагирования на ЧС), 102 (служба полиции), 103 (служба скорой медицинской помощи), 104 (служба газовой сети)
Единый телефон доверия ГУ МЧС России по Оренбургской области
Источник