Earth Curvature Calculator
Accurately calculate the curvature you are supposed to see on the ball Earth.
| Distance | Curvature |
|---|---|
| 1 km | 0.00008 km = 0.08 meters |
| 2 km | 0.00031 km = 0.31 meters |
| 5 km | 0.00196 km = 1.96 meters |
| 10 km | 0.00785 km = 7.85 meters |
| 20 km | 0.03139 km = 31.39 meters |
| 50 km | 0.19620 km = 196.20 meters |
| 100 km | 0.78479 km = 784.79 meters |
| 200 km | 3.13897 km = 3138.97 meters |
| 500 km | 19.6101 km = 19610.09 meters |
| 1000 km | 78.3196 km = 78319.62 meters |
| Distance | Curvature |
|---|---|
| 1 mile | 0.00013 miles = 0.67 feet |
| 2 miles | 0.00051 miles = 2.67 feet |
| 5 miles | 0.00316 miles = 16.67 feet |
| 10 miles | 0.01263 miles = 66.69 feet |
| 20 miles | 0.05052 miles = 266.75 feet |
| 50 miles | 0.31575 miles = 1667.17 feet |
| 100 miles | 1.26296 miles = 6668.41 feet |
| 200 miles | 5.05102 miles = 26669.37 feet |
| 500 miles | 31.5336 miles = 166497.53 feet |
| 1000 miles | 125.632 miles = 663337.65 feet |
Explanation:
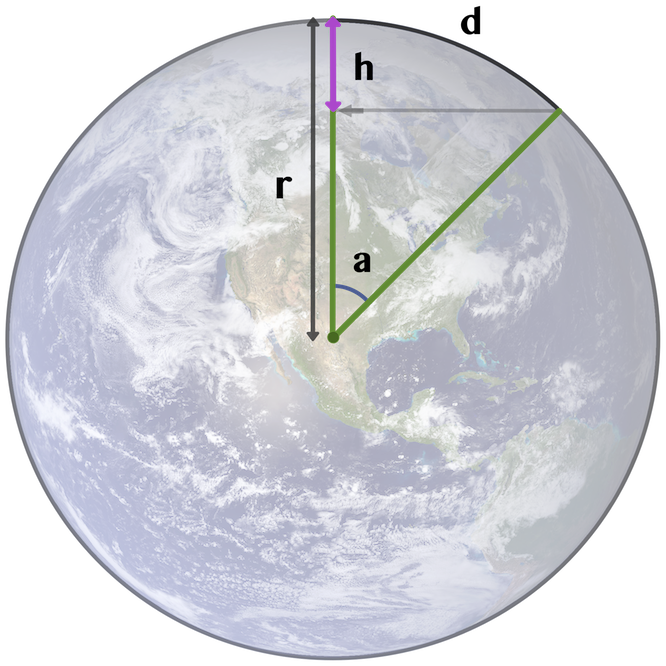
The Earth’s radius (r) is 6371 km or 3959 miles, based on numbers from Wikipedia,
which gives a circumference (c) of c = 2 * π * r = 40 030 km
We wish to find the height (h) which is the drop in curvature over the distance (d)
Using the circumference we find that 1 kilometer has the angle
360° / 40 030 km = 0.009° . The angle (a) is then a = 0.009° * distance (d)
The derived formula h = r * (1 — cos a) is accurate for any distance (d)
Note: Using the formula 8 times the distance in miles squared is not accurate for long distances but is fine for practical use.
Источник
Earth Curvature Calculator
This Earth curvature calculator allows you to determine how much of a distant object is obscured by the Earth’s curvature. So, if you ever wanted to be able to estimate the total height of a target that is partially hidden behind the horizon, now you can. You will also be able to find out you how far you can see before the Earth curves – that is, what is your distance to the horizon.
Don’t worry if you don’t know what the curvature of Earth is yet – simply keep reading to learn all the necessary information!
What is the Earth’s curvature
Imagine you are looking at the sea. There is no land in sight, only the endless blue waters, shimmering in the afternoon sun. You can make out the line that divides the sea and the sky. This line is called the horizon.
Suddenly, you begin to see a point that is getting larger and larger. First, it is a top of a white sail; when it moves closer, you can also notice the shape of a ship. Where was this ship before? It was hidden behind the horizon.
The reason for this is obvious: as Earth’s shape is very similar to a sphere – the surface between you and the ship is not completely flat, but «bulges» up a bit. This is why it has obstructed your view. The curvature of Earth is simply the measure of this «bulge». It is expressed as the height of the «bulge» per kilometer or per mile.
Curvature of Earth per mile
How large is the curvature of Earth, then? As we don’t notice it in our everyday lives, it has to be quite small. Most sources consider 8 inches per mile as the most accurate estimate. This means that for every mile between you and an object, the curvature will obstruct 8 inches of the object’s height.
How far can I see before the Earth curves?
The first thing you can find with our Earth curvature calculator is the exact distance between you and the horizon. You only need to know two values: your eyesight level (in other words, the distance between your eyes and mean sea level – assuming you are looking out to sea) and the radius of the Earth. Input these numbers into the following equation:
- a – Distance to the horizon;
- h – Eyesight level above mean sea level, and
- r – Earth’s radius, equal to 3959 miles or 6371 km.
This equation can be derived using the Pythagorean theorem. You can try to derive it yourself – it is not that hard!
Calculating the obstructed height of an object
Look at the image above. It represents a situation analogical to the one with the ship from above. You can see a part of the object, but the rest of it is hidden behind the horizon. If you want to know the height of the object that is obstructed, simply enter all the necessary values into the Earth curvature calculator. You can also calculate the height manually:
Determine the distance between you (the observer) and the lowest point of the object that you can actually see. Let’s call this value d and assume it is equal to 25 miles.
Measure your eyesight level – that is, the height at which your eyes are above the sea. We will denote it with a letter h . We can assume that it is equal to 6 feet, which is approximately 0.0011 miles.
Calculate the distance between you and the horizon, a , using the aforementioned formula:
a = √[(r + h)² — r²] = √[(3959 + 0.0011364)² — 3959²] = 3 miles
Now, you can input these values to the second formula to find the height of the obstructed part of the object x :
x = √(3² — 2*3*25 + 25² + 3959²) — 3959
If you have trouble with units conversion, simply use our length converter.
Is this Earth curvature calculator accurate?
You might find that if you were to test our calculator vs. a real life scenario, our calculator might be slightly wrong in some cases. Why does this happen? Does it mean the Earth is flat and doesn’t curve at all?
Of course not! It just means that our calculator doesn’t account for the phenomenon of refraction. When light travels through a medium which is not perfectly uniform, such as air, it bends, or refracts. This can happen when light hits a pocket of cold air, or a hot draft of rising air.
As the ray of light bends slightly, it changes direction. This means that some photons from the object that would usually hit the ground can bend around the Earth’s surface and reach your eye, so the heights and distances as shown in the picture above may seem to be different. That’s why, when you are calculating the obstructed height of an object, the distances you see may be a bit different from the observed ones!
Источник
Видимый горизонт и дальность видимости
Расчет видимого горизонта и дальности видимости в зависимости от высоты наблюдателя и наблюдаемого объекта.
Калькулятор ниже предназначен для расчета видимого горизонта и дальности видимости в зависимости от высоты наблюдателя и наблюдаемого объекта. Под ним, как водится, немного теории.
Видимый горизонт и дальность видимости
Видимый горизонт
Так как земля изогнута, наблюдателю, находящемуся, например, в море, представляется, что он находится в центре круга, по краям которого небо как бы смыкается с морской поверхностью. Эта окружность и называется видимым горизонтом наблюдателя. На картинке слева видимый горизонт обозначен пунктирной линией. То есть для наблюдателя, находящегося в точке А на высоте h от земли, видимый горизонт будет образован всеми точками касания лучей зрения земной поверхности (угол BCO равен 90 градусов).
Говоря о видимом горизонте чаще всего имеют в виду длину d отрезка BC. Длину d легко вывести из теоремы Пифагора.
где R — радиус Земли, который обычно принимают за 6378 километров.
В реальной жизни на стороне человека выступает атмосфера. Она, благодаря явлению рефракции, то есть преломлению лучей в верхних слоях атмосферы, расширяет его горизонты примерно на 6% 🙂
Формула, таким образом, принимает вид
В принципе, везде (по крайней мере, насколько я находил в Интернете) для расчетов используют упрощенную формулу, из которой исключен радиус Земли. Она, кстати, вполне выводится из верхней.
, для результата в морских милях или
, для результата в километрах
Дальность видимости
Дальность видимости предметов определяется наибольшим расстоянием, на котором наблюдатель увидит вершину наблюдаемого объекта на линии горизонта. Как видно из рисунка, она зависит как от высоты наблюдателя, так и от высоты наблюдаемого объекта. Собственно, это сумма дальности видимого горизонта наблюдателя и дальности видимого горизонта наблюдаемого объекта. Это довольно важный параметр для навигации.
В калькуляторе я ее вычисляю, а на практике, насколько я понимаю, дальности видимости береговых ориентиров указываются во всяческих лоциях, мореходных таблицах и тому подобном для высоты наблюдателя, равной пяти метрам. Для поправки на фактическую высоту наблюдателя используется «номограмма для расчета дальности видимости предметов в море в дневное время при среднем состоянии атмосферы».
Источник
Curvature Calculator + Earth Curvature Formula
Surveyors and maritime businesses deal with measurements involving the Earth’s curvature. Using formulas and surveying instruments, they can determine the part of a distant object which gets obscured by this curvature. This allows them to come up with a good estimate of the total height of an object that’s partially hidden by the horizon. In such a case, this curvature calculator comes in handy for quick calculations.
How to use the curvature calculator?
This curvature calculator is as simple as they come. As long as you have the required values, you can use this online tool without having to calculate by hand using the Earth curvature formula. Here are the steps to follow:
- First, enter the value of the Distance to the Object and choose the unit of measurement from the drop-down menu.
- Then enter the value of the Eyesight Level and choose the unit of measurement from the drop-down menu.
- After entering both values, the Earth curvature calculator automatically generates for you the value of the Distance to Horizon and the value of the Obscured Object Part.
What is the curvature of the Earth?
Imagine yourself looking far at an open sea where you see no land, only the seemingly endless blue water. On clear days, you may see the horizon dividing the sky and the sea. Maybe by chance, you would also see a certain point on the horizon that starts to get bigger and bigger.
As it draws closer, you discover that it’s a ship and the first thing you would notice is its sail. The closer it gets, the more the shape of the ship becomes distinct. Before you can make such a sighting, you can ask yourself the questions, “Where was the ship before it made its gradual appearance?” and “Was it concealed by the horizon?”
At this point, we already know that the Earth is a sphere and not flat. Therefore, between the ship and yourself, it does bulge up quite a bit. This is the reason why it obstructed you from the view. This “bulge” is what’s known as the Earth’s curvature. You measure this value as the height of the “bulge” per mile or kilometer.
How to calculate the curvature of the Earth?
The degree of obstruction of a distant object caused by the curvature of the Earth is dependent on several factors namely:
- The object’s distance.
- The observer’s height.
- The object’s height.
- The magnitude of atmospheric refraction.
“Flat-Earthers” or those people who still believe that the Earth is flat, prefer using the visibility of faraway objects so they can prove that the curvature of the Earth is just a myth. Of course, as you would expect, their theories fail because they don’t take into account the observer’s height and the atmospheric refraction.
Aside from these factors, they also make a few more mistakes like errors in unit conversion, errors in distance calculation, and so on. If only these flat-Earthers gave these due considerations and they tried to fix their mistakes, everything should turn out differently. They would then discover that we have a spherical Earth.
Not taking into account the observer’s height is the most common mistake when calculating the Earth’s curvature whether you use a curvature calculator or the Earth curvature formula. All that is usually done is to calculate the drop from a horizontal plane.
Even if you use a professional-grade AutoCAD software which is highly precise, the resulting numbers will still turn out incorrect if you made a mistake in the geometry in the first place.
Not accounting for atmospheric refraction is another very common mistake. Atmospheric refraction refers to the deviation of light from a straight line as it passes through the atmosphere due to the variation in air density as a function of height.
In simpler terms, atmospheric refraction usually bends light to follow the Earth’s curvature to a specific point. This causes an object to appear higher above the horizon than it actually is. It’s also important to note that atmospheric refraction is never a constant as it would depend on weather conditions and how much refraction may vary in one day.
If you have taken all of this information into consideration and you have corrected all mistakes, you will be able to find the values you need through a simple process. Here is how to calculate for the Earth’s curvature without using a curvature calculator:
For this example, let’s assume that the Earth has a spherical shape with a radius of 3,963 miles. If you’re at point P on the surface of the Earth, then move tangent to the surface a distance of one mile, in order to form a right triangle. Then using the Pythagorean theorem:
c² = a² + b²
c² = (3963)² + (1)²
c² = 15705370
Then take the square root of both sides of the equation:
You should also solve for your position above the Earth’s surface:
P = 3963.000126 – 3963
P = 0.000126 miles
P = 7.98 inches
This result means that the surface of the Earth curves at approximately 8 inches for every mile.
How much does the Earth curve per mile?
The Earth does have a curvature but almost nobody ever notices it because the value is very small. For those in the know, the most precise value of curvature is about 8 inches per mile. This means that for each mile of distance between you and another object, the curvature obstructs approximately 8 inches of the object’s height.
How far can you see Earth curvature?
The Earth curvature calculator yields the distance between yourself and the horizon. There are only two values needed to solve this, namely the level of your eyesight or the distance between the ground and your eyes and the Earth’s radius. Enter these values into the curvature equation:
where
a refers to the distance to the horizon
h refers to the level of your eyesight
r refers to the radius of the Earth which is 3963 miles
The equation itself comes from the Pythagorean Theorem. You can even try deriving the equation yourself, it isn’t that difficult!
Источник