Формулы радиуса орбиты, орбитальной скорости и пер
Формулы для расчета радиуса орбиты, скорости орбитального движения и периода планет.
При расчетах используются величины:
— радиус орбиты R (при условном круговом движении) в а.е.
— период T (земной год)
— орбитальная скорость V а.е./год
1. Соотношение радиуса и скорости.
Произведение радиуса и квадрата скорости для всех планет одинаково.
R V2 = const
(получается от преобразований третьего закона Кеплера: R3/ T2 const)
R V2 = R V2 — для разных радиусов обрит разных планет и разных радиусов кривизны одной планеты.
производим вычисления:
для Земли — 1 х 6.28 х 6.28 / 1 = 39.434
где V — 2х 3.14 х R / T 2 х 3.14 х 1 : 1 = 6.28 а.е. /год
для Марса 1.532 х 5.07 х 5.07 = 39.379
скорость для марса : 2 х 3.14 х 1.52 : 1.88 = 5, 07 а.е. / год
радиус орбиты Марса взят средний — он колеблется от 1.405 (перигелий) до 1.693 (афелий)
для Юпитера 5.2 х 2.75 х 2.75 = 39.325
скорость 2 х 3.14 х 5.2 : 11.86 = 2.75 а.е. / год
2. Соотношение радиуса орбиты и периода.
Для вычисления периода по радиусу орбиты можно использовать следующую формулу:
Радиус, умноженный на корень квадратный из радиуса, дает период.
(Если единица измерения радиуса — а.е.
то период получается в земных годах.)
получается, что для каждой планеты есть некое число, которое умноженное на себя дает радиус орбиты, а умноженное на себя еще раз — дает период.
Для Марса это число примерно 1.232, для Юпитера 2.28, для Урана 4.38,
для Плутона 6.26 , для Венеры 0.85
Получается числовой ряд планет:
Меркурий 0.62 0.387 0.24
Венера 0.85 0.723 0.615
Земля 1 1 1
Марс 1.232 1.52 1.88
Юпитер 2.28 5.2 11.86
Сатурн 3.09 9.58 29.6
Уран 4.38 19.18 84.048
где: первое это некое базовое число; второе радиус; третье период.
зависимость:1 — число, 2- число возведенное в квадрат, 3- возведенное в куб.
Базовое число планеты — соотношение скоростей Земли и планеты.
А соотношение скоростей Земли и планеты получается из соотношения квадратных корней радиусов этих планет.
Теперь, если взять, например, орбитальную скорость Земли за единицу,
то орбитальная скорость Земли относительно скорости Марса 1.2328.
тогда: радиус обриты Марса есть 1.2328 х 1.2328 = 1.52 а.е.
а период орбиты Марса 1.52 = 1.2328 = 1.8739 в земных годах
что в упрощенной записи :
Vз : V м (Vз :V м ) 2 = R (Vз :V м ) 2 х R = T
или n , далее n в квадрате и n в кубе.
где n Vз :V м — отношение скоростей Земли и Марса.
R V2 = const (получается от преобразований третьего закона Кеплера)
Для понимания сути движения планет интересно сделать ещё и такое построение.
Все планеты СС одновременно движутся по своим орбитам. Если взять некий общий отрезок времени,то каждая из планет пройдет за это время по орбите своё раcстояние.
Если на основе этого расстояния, построить квадрат, то площадь этого квадрата для каждой планеты будет пропорциональна орбитальной скорости.
И, если площадь этого квадрата умножить на радиус орбиты, то для всех планет получится одинаковое число, выражающее объём.
И получиться некая константа трехмерного пространства.
Это можно выразить так:
Квадрат расстояния пройденной каждой планетой за общую единицу времени обратно пропорционален радиусам их орбит или произведение радиуса обриты на квадрат расстояния для всех планет за общую единицу времени есть величина одинаковая.
5. Период соединения.
Есть ещё одна формула которая позволяет вычислить через какое время произойдет соединение планет планеты.
Т1 х Т2 / Т2-Т1
6. И, конечно, каждая планета за одну единицу времени проходит угол (сектор), который по отношению к земному, обратно пропорционален периодам.
Формулы могут применяться и для расчета параметров движения спутников.
На рисунке: Таблица соотношения параметров планет Солнечной системы относительно Земли.
комментарии к таблице.
Данные для других планет выражен по отношению к параметрам дв. Земли.
Соотношение скоростей мы понимаем, как соотношение путей пройденных планетой по своей орбите за единицу времени. Соотношение скоростей, возведенное в квадрат дает соотношение радиусов, а возведенное в куб — соотношение периодов планет.
Источник
Наблюдение искусственных спутников Земли
Глава 1: Как движутся ИСЗ?
Перед тем, как приступить к рассмотрению вопросов наблюдения ИСЗ, нужно выяснить как они движутся — по каким орбитам и каковы характеристики этих орбит. Без понимания этих вопросов наблюдение ИСЗ превращается в охоту за неведомым зверем, который неизвестно где обитает.
§ 1. Законы Кеплера и типы орбит
Из курса средней школы нам известно, что тело, движущееся по орбите вокруг другого тела, подчинено трём законам Кеплера. Нас будут интересовать только два из них — первый и третий.
Согласно первому закону Кеплера, тело, обращающееся вокруг Земли (в нашем случае) движется по эллипсу, в одном из фокусов которого находится центр Земли (см. рис. 2). Мы специально не упоминали тут, что тело может двигаться по трём видам орбит — эллипс, гипербола и парабола. Нас интересуют только периодические орбиты, а из перечисленных такой является эллипс.
Элементы эллипса показаны на рис. 2. «F1« и «F2« — фокусы эллипса; «a» — большая полуось; «b» — малая полуось; «е» — эксцентриситет эллипса, который определяется следующим образом:

Таким образом, первое важное положение — ИСЗ движутся вокруг Земли по эллипсам .
Согласно третьему закону Кеплера, квадраты периодов обращения «T» спутников относятся как кубы их больших полуосей «a»:
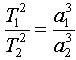
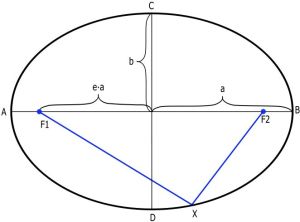 |
| Рис. 2. Элементы эллипса. [2] |
§ 2. Орбитальные элементы
Для того, чтобы задать параметры и ориентацию орбиты ИСЗ в пространстве, нужно указать 6 т.н. кеплеровских элементов (орбитальных элементов) (см. рис. 3):
- Большая полуось «a». Равна среднему расстоянию ИСЗ от центра Земли.
- Эксцентриситет «e» (см. формулу 1) — мера сплюснотости эллипса.
- Наклонение орбиты «i» к экваториальной плоскости Земли — угол пересечения плоскости орбиты ИСЗ с плоскостью экватора Земли. Отсчитывается против часовой стрелки, если смотреть со стороны восходящего узла орбиты. Измеряется от 0° до 180°. Если наклонение не более 90°, то движение спутника считается прямым, если более 90° — то обратным.
- Аргумент перигея (АП) ω — угол, отсчитываемый в плоскости орбиты ИСЗ от восходящего узла орбиты до точки перигея (точка, где расстояние между ИСЗ и центром Земли наименьшее). Угол отсчитывается против часовой стрелки, если смотреть с северного полюса мира. Линия, соединяющая восходящий и нисходящий узлы называется линией узлов.
- Долгота восходящего узла (ДВУ) Ω — угол, отсчитываемый в плоскости земного экватора от восходящего узла до точки весеннего равноденствия. Угол отсчитывается против часовой стрелки, если смотреть с северного полюса мира.
- Средняя аномалия (СА) M0 — угол, отсчитываемый в плоскости орбиты ИСЗ от перигея до ИСЗ на орбите. Угол отсчитывается против часовой стрелки, если смотреть с северного полюса мира.
 |
| Рис. 3. Орбитальные элементы. [2] |
Итак, наше второе важное положение — орбита ИСЗ полностью задаётся шестью орбитальными элементами .
§ 3. Круговая орбита
Рассмотрим частный случай эллиптической орбиты — круговая орбита. Если значение эксцентриситета орбиты ИСЗ е = 0, то орбита представляет собой окружность с центром в центре Земли.
Для того, чтобы тело стало спутником Земли, оно должно обладать определённой скоростью при полёте вокруг неё. Если бы у Земли не было атмосферы, то минимальная скорость, необходимая для того, чтобы тело двигалось по окружности вокруг Земли, равна vк0 = 7,91 км/с. Но в реальности такого быть не может — спутник будет сильно тормозится в атмосфере Земли. Если ИСЗ начнёт двигаться на высоте менее примерно 160 км от поверхности Земли, то он сможет сделать лишь пару оборотов, после чего начнёт необратимо терять скорость и сгорит в плотных слоях атмосферы. Для примерного расчёта скорости ИСЗ на круговой орбите можно воспользоваться формулой [1]:

где R = 6371 км — средний радиус Земли, r = R + h — расстояние от центра Земли до ИСЗ, h — высота ИСЗ над поверхностью Земли. При наблюдениях важно знать период обращения ИСЗ Т — время, необходимое на один полный оборот вокруг Земли. Для круговой орбиты период Т можно вычислить по формуле [1]:

Из (4) видно, что минимальное время, необходимое ИСЗ для одного оборота, равно Tк0 = 84,4 минуты — при нулевой высоте над поверхностью. Никакое тело не может быстрее обогнуть поверхность Земли. При примерных оценках периода обращения ИСЗ по круговой орбите полезно помнить, что период обращения увеличивается примерно на 1 минуту при увеличении высоты ИСЗ на каждый 50 км. Этой оценкой можно пользоваться для ИСЗ не выше 1000 км.
Наше третье важное положение — ИСЗ не может двигаться долгое время по орбите вокруг Земли ниже 140-160 км. При этом, период обращения по круговой орбите является минимальным и для диапазона высот 160-1000 км изменяется всего с 87,6 до 105 минут .
§ 4. Эллиптическая орбита
Теперь рассмотрим общий вид орбиты ИСЗ — эллиптическая орбита (см. рис. 4). Как было указано выше, из первого закона Кеплера следует, что в фокусе эллиптической орбиты будет находится Земля (З), вокруг которой вращается ИСЗ. Двигаясь по эллиптической орбите, ИСЗ ближе всего подлетает к центру Земли в точке «П» — в перигее, а дальше всего находится в точке «А» — в апогее. Линия, соединяющая перигей и апогей называется линией апсид. Из наблюдений ИСЗ можно определить большую полуось и эксцентриситет орбиты, из которых можно вычислить значения перигейного «q» и апогейного «Q» расстояний:

 |
| Рис. 4. Перигей и апогей. |
Из (5) видно, что Q + q = 2a. При движении по орбите изменяется расстояние «r» от Земли до ИСЗ — величина радиус-вектора «r» задаётся выражением [3]:
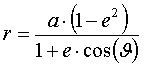
Скорость ИСЗ в любой точке эллиптической орбиты задаётся выражением [2]:
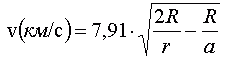
Период обращения для спутника на эллиптической орбите вычисляется по формуле (4), в которой вместо «r» нужно подставить значение большой полуоси «a».
Наше четвёртое важное положение — скорость движения ИСЗ по эллиптической орбите не равномерна: максимальна она в перигее, а минимальна в апогее. Период обращения теперь определяется не только большой полуосью «a», но и значением эксцентриситета «e» .
§ 5. Эволюция орбиты ИСЗ
В этом параграфе мы рассмотрим, как изменяются параметры реальной орбиты ИСЗ под воздействием определённых факторов.
Прежде всего следует отметить следующее: если бы Земля имела форму идеального шара с равномерным распределением вещества, была лишена атмосферы, а Луна и Солнце отсутствовали бы, то ИСЗ вечно бы вращался по своей орбите, ориентация которой в пространстве не изменялась. Если бы спутник совершал 14 оборотов в сутки (при этом его период равен примерно 103 минуты), то за время одного витка ИСЗ Земля повернётся на 1/14 полного оборота (это примерно 26°). Это означает, что с каждым новым траектория ИСЗ смещалась к западу на 26° за каждый виток.
Прецессия орбиты
В реальности форма Земли — геоид, полярный радиус которого RП = 6356,8 км, а экваториальный — RЭ = 6378,2 км, т.е. экваториальный радиус больше полярного на 21,4 км. Земля имеет экваториальный «горб», который своей массой оказывает влияние на движение ИСЗ. Влияние это не такое уж явное — масса «горба» не вызывает изменения наклонения «i» орбиты за счёт притягивания плоскости орбиты к плоскости экватора, как можно было бы ожидать — плоскость орбиты медленно поворачивается вокруг земной оси в направлении, противоположном вращению ИСЗ (см. рис. 5).
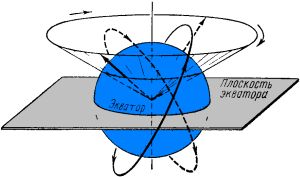 |
| Рис. 5. Прецессия орбиты ИСЗ [4]. |
Этот процесс называется прецессией. Угол прецессии плоскости орбиты ИСЗ остаётся неизменным. Угловая скорость прецессии «X1« (градусов в сутки) определяется, в основном, наклонением орбиты [1]:
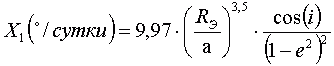
где «i» — наклонение орбиты, «e» — эксцентриситет, RЭ — экваториальный радиус Земли, «а» — большая полуось орбиты ИСЗ. Если спутник движется в запада на восток, орбита поворачивается с востока на запад. Чем меньше наклонение ИСЗ, тем больше значение прецессии (см. рис. 6). Если спутник вращается с востока на запад (обратное движение ИСЗ), то прецессия орбиты происходит в обратную сторону. При этом линия узлов также поворачивается (см. рис. 7).
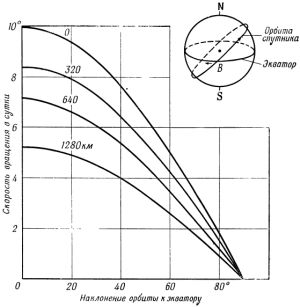 |
| Рис. 6. Скорость вращения плоскости орбиты ИСЗ за счёт прецессии. Числа у кривых указывают значение большой полуоси [1]. |
 |
| Рис. 7. Смещение восходящего узла за один виток [4]. |
Теперь посмотрим, к каким изменениям условий наблюдения спутника приводит прецессия. Как известно, Земля делает полный оборот за 23 ч 56 м 4,09 с (звёздные сутки) — за 24 ч (средне-солнечные сутки) небо нам кажется повернувшимся на 361° (т.к. звёздные сутки короче средне-солнечных на 4 минуты — за это время небо повернётся на 1°). Если бы плоскость орбиты ИСЗ не прецессировала, то через 24 ч он появлялся бы на небе на 1° западнее, чем накануне (если движение ИСЗ прямое). Но за счёт прецессии орбита поворачивается на Х1 градусов за сутки, поэтому ИСЗ через 24 ч окажется на Х1 + 1 градус западнее (при обратном движении — на 1 — Х1 градус к западу). Период обращения спутника не кратен целой части суток. Если через сутки спутник будет пересекать ту же широту Земли на n минут позже, он окажется ещё на n/4 градусов западнее, т.к. за 1 минуту Земля поворачивается на 1/4 минуты. Следовательно, суммарный суточный сдвиг к западу составит (Х1 + 1 + n/4) градусов [1].
Вращение эллиптической орбиты
Следующим важным эффектом, влияющим на эволюцию орбиты ИСЗ, является поворот плоскости эллиптической орбиты. Эффект этот, как и предыдущий, обязан своим существованием экваториальному «горбу» Земли, но в отличие от прецессии, действует только на эллиптичные орбиты. Эффект заключается в том, что эллиптическая орбита постоянно поворачивается в своей плоскости вперёд для спутников с нулевым наклонением, и назад — для спутников с наклонением, близким к 90°. За счёт этого точки перигея движутся вперёд или назад по орбите (см. рис. 8).
 |
| Рис. 8. Поворот эллиптической орбиты [1]. |
Скорость вращения «X2« эллиптической орбиты определяется выражением [1]:

На рис. 9 показаны графики зависимости X2(i) для ИСЗ с разными значениями больших полуосей «a».
 |
| Рис. 9. Скорость вращения X2 эллиптической орбиты [1]. |
Вращение происходит в том же направлении, что и движение спутника, если наклонение i 63,4°. При i = 63,4° поворот орбиты отсутствует.
Наше пятое важное положение — движение ИСЗ подвержено возмущениям из-за несферичности Земли. За счёт прецессии орбита спутника может смещаться с угловой скоростью до 9°/сутки, а за счёт поворота эллиптической орбиты — до 15°/сутки. При этом, чем меньше наклонение, тем сильнее оба эффекта, но действовать они могут как в одну сторону, так и в противоположные .
Атмосферное торможение
Прецессия орбиты и поворот её плоскости связаны с действием несферичности Земли. Но кроме этого Земля окружена атмосферой, которая прослеживается до 2000 км над её поверхностью. Из этого следует, что на движение ИСЗ, особенно на низких орбитах, влиянием атмосферы мы пренебрегать не можем. Атмосферное давление падает с высотой экспоненциально — на высоте 200 км оно составляет 10 -12 мбар (на уровне моря атмосферное давление составляет 1013 мбар), а на высоте 900 км — уже только 10 -42 мбар [6]. Тем не менее, даже такая разреженная атмосфера может приводить к изменению орбиты ИСЗ.
Сила сопротивления движущемуся в атмосфере телу определяется выражением [4]:

где «cx« — безразмерный коэффициент сопротивления, для верхней атмосферы равный 2-2,5; «S» — площадь максимального сечения спутника, перпендикулярного налетающему воздушному потоку; «v» — скорость ИСЗ, «ρ» — плотность атмосферы на высоте полёта ИСЗ. Торможение ИСЗ определяется его парусностью — чем больше площадь и меньше масса, тем больше торможение.
Для спутника, движущемся по круговой орбите, сопротивление атмосферы будет сказываться следующим образом: спутник будет медленно опускаться по спирали с постоянно увеличивающейся скоростью. Угол снижения спутника на круговой орбите можно оценить из выражения [1]:
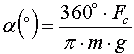
где «m» — масса ИСЗ, «g» — ускорение свободного падения. Снижение по спирали будет продолжаться до тех пор, пока спутник не опустится до высоты 160 км — ниже этой высоты сила сопротивления настолько велика, что спутник начинает резкое снижение и сгорит в атмосфере. На высоте 160 км период обращения равен примерно 88 минут — любой ИСЗ с меньшим периодом обречён.
Если орбита эллиптическая, то результат действия сопротивления атмосферы будет следующим: т.к. сопротивление сильно уменьшается с высотой, то максимальное сопротивление ИСЗ будет испытывать в перигее, а минимальное — в апогее. Это слабо меняет высоту перигея, но уменьшает высоту апогея — в результате эллиптичность орбиты уменьшается и спутник начинает спуск по спирали. На рис. 10 показано снижение ИСЗ в случае эллиптической орбиты.
 |
| Рис. 10. Снижение спутника в атмосфере [4]. |
Оценить время жизни спутника можно из выражения (12) [1]:

где e0 — начальный эксцентриситет орбиты, T0 — начальный период обращения, ΔT — суточное изменение периода. Тогда измение периода будет определятся выражением [1]:

а изменение эксцентриситета [1]:

Формулы (13) и (14) справедливы для значений e = 0,02-0,2. На атмосферное торможение сильно влияет время суток (в подсолнечной точке атмосфера подымается выше), а также активность Солнца.
Как видно, время жизни спутника определяется его эксцентриситетом и большой полуосью. В таблице ниже представлены времена жизни ИСЗ для разных значений перигея и апогея [5]:
| Время существования ИСЗ массой 100 кг и диаметром 1 метр, сутки | |||||
| Высота перигея, км | Высота апогея, км | ||||
| 500 | 700 | 1000 | 1300 | 1600 | |
| 200 | 9 | 18 | 37 | 58 | 82 |
| 230 | 25 | 52 | 102 | 165 | 237 |
| 260 | 53 | 116 | 238 | 370 | 535 |
| 300 | 114 | 260 | 545 | 890 | 1280 |
| 400 | 410 | 1120 | 2630 | 4450 | 6600 |
Наше шестое важное положение — сопротивление атмосферы Земли вызывает уменьшение большой полуоси орбиты ИСЗ, в результате чего он по спирали спускается вниз. При достижении высоты около 160 км спутник сможет сделать всего пару оборотов и сгорит в атмосфере, войдя в резкий и необратимый спуск .
Давление света
Впервые идею о том, что свет производит давление на тела, высказал в 1619 г. И. Кеплер — для объяснения эффекта отклонения кометных хвостов от Солнца. Современная теория даёт значение давления следующим выражением (формула Максвелла-Бартоли) [3]:
где «E» — мощность электромагнитного излучения, приходящаяся на единицу площади тела, «η» — коэффициент отражения тела, «c» — скорость света. Для абсолютно поглощающего тела вблизи Земли давление света равно 4,3 · 10 -6 Н/м 2 . Для абсолютно отражающего тела эта величина в два раза больше. Световое давление становится ощутимым для лёгких спутников выше 500 км, т.к. ниже большее значение имеют колебания плотности атмосферы.
В заключении параграфа нужно отметить, что перечисленные факторы влияния на эволюцию орбиты спутника не составляют полный список. Например, на ИСЗ воздействуют своим притяжением Солнце и Луна, но это воздействие в 10000 раз слабее действия экваториального «горба» Земли, но его нужно учитывать для орбит с большим эксцентриситетом. Экваториальный «горб» также вызывает незначительные колебания плоскости орбиты ИСЗ при пересечении экваториальной плоскости. Наконец, неравномерность распределения масс под поверхностью Земли также сказывается на движении спутника.
Как видим, движение спутника не так просто, как может показаться на первый взгляд. В наше время расчёты эволюции орбиты значительно упростились с точки зрения затраты времени, т.к. современные компьютеры имеют огромную вычислительную мощность. Даже любители, используя специальные программы (см. далее), могут довольно точно расчитывать положение спутников на нужную им дату и время, причём на любой промежуток времени — в начале космической эры любители могли об этом только мечтать.
Источник