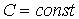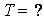Предположим что земля просверлена по диаметру

2016-11-25
Сквозь Землю по диаметру прорыли сквозную шахту. Пренебрегая вращением Земли и сопротивлением, определить характер движения тела, брошенного в шахту.

Запишем закон Ньютона для тела в шахте на расстоянии $x$ от центра Земли:

Можно показать, что сила со стороны внешнего шарового слоя толщиной $R — x$ равна нулю. Таким образом, сила, действующая на тело со стороны Земли:

$M$ — масса Земли, сосредоточенная в шаре радиуса $|x|$ (плотность Земли $\rho = \frac>< \frac<4> <3>\pi R^<3>>$ ).

Из (2, 3) с учетом $g = \fracM_<0>>$ находим:

Непосредственно убеждаемся, что

правильно описывает выражение для проекции силы $\vec$ на ось $x$ (из рисунка видно, что при $x > 0 F_ 0$).

Подставляя $a_ = x^< \prime \prime>$ и (6) в (5), получаем:

Это уравнение для гармонических колебаний с периодом

Таким образом, движение тела в шахте — гармонические колебания с периодом $T$ из (7).

Докажем, что гравитационная сила, действующая на тело внутри тонкой сферической оболочки, равна нулю.

Каждому малому фрагменту оболочки площадью $S$ соответствует фрагмент площадью $S^< \prime>$. Из геометрических соображений следует:

где $r$ и $r^< \prime>$ — расстояния от тела до фрагментов $S$ и $S^< \prime>$ соответственно. Обозначим массу на единицу поверхности оболочки через $\sigma$ и запишем закон всемирного тяготения для взаимодействия тела с фрагментами $S$ и $S^< \prime>$:

С учетом (8) из соотношений (9) находим: $F = F^< \prime>$. Отсюда получаем искомое утверждение.

Поскольку шаровой слой можно представить как набор тонких сферических оболочек, приходим к утверждению о том, что сила со стороны шарового слоя, действующая на тело внутри его, равна нулю.

Источник

Примеры решения задач по механике , страница 14

м

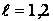
АНАЛИЗ. Задача на упругие колебания стержня вокруг вертикальной оси, проходящей через неподвижный центр стержня. Незначительность угла предварительного поворота стержня позволяет считать последующие за этим колебания с малой амплитудой гармоническими.

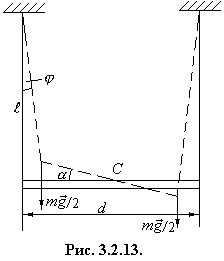
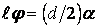
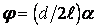
РЕШЕНИЕ. Стержень повернули на малый угол a вокруг вертикальной оси, проходящей через центр масс стержня. При этом нить отклонилась на угол j, причем , т.е.

, (3.2.47)

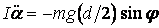
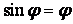
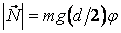
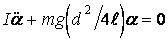
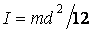
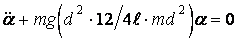
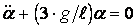
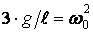
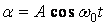
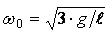
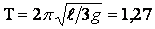
После того как нить отпустили, стержень начал совершать малые колебания. Уравнение колебаний имеет вид: , т.к. для малых колебаний , возвращающий момент силы . Учитывая (3.2.47), получим , где I – момент инерции стержня относительно точки С, т.е. . В результате

, далее . Обозначим . Уравнение колебаний имеют вид: , где , а с.

ОТВЕТ: 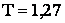с.

3.2.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1. Маятник состоит из медной проволоки диаметром d₁ = 0,1 мм и медного шарика диаметром d₂ = 3 см. На сколько процентов увеличится период колебания, если заменить медный шарик свинцовым того же диаметра. Амплитуду считать малой.

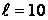
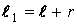
2. Шар, радиус которого r = 5 см подвешен на нити длиной см. Определить погрешность, которую мы делаем, приняв его за математический маятник с длиной =15 см.

3. Некоторое тело качается около оси с периодом Т₁ = 0,5 с. Если же к нему прикрепить грузик с массой m = 50 г на расстоянии 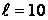см ниже оси, то оно качается с периодом Т₂ = 0,6 с. Найти момент инерции тела относительно оси качания.

4.Определить период колебаний массы m = 121 г ртути, находящейся в U – образной трубке. Площадь сечения трубки S = 0,3 см 2 .

5. Шарик катается по дну сферической чашки. Предполагая, что эти колебания можно считать синусоидальными, определить их период. Считать радиус чашки равным R, радиус шарика r.

6. Предположим, что по одному из диаметров Земли просверлена шахта. Принимая Землю за однородный шар с плотностью r = 5,5×10 3 кг/м 3 : а) показать, что при отсутствии трения тело, падающее в этой шахте, совершает гармонические движения; б) найти время t движения тела от поверхности Земли до ее центра.

7. Два диска могут вращаться около осей, являющихся продолжением одна другой. Моменты инерции дисков относительно этой оси равны J₁ и J₂. Диски соединены пружиной, коэффициент кручения которой равен G. Определить период, с которым будут колебаться диски, если их повернуть в противоположных направлениях, закручивая при этом пружину, и отпустить.

АлтГТУ 419

АлтГУ 113

АмПГУ 296

АГТУ 267

БИТТУ 794

БГТУ «Военмех» 1191

БГМУ 172

БГТУ 603

БГУ 155

БГУИР 391

БелГУТ 4908

БГЭУ 963

БНТУ 1070

БТЭУ ПК 689

БрГУ 179

ВНТУ 120

ВГУЭС 426

ВлГУ 645

ВМедА 611

ВолгГТУ 235

ВНУ им. Даля 166

ВЗФЭИ 245

ВятГСХА 101

ВятГГУ 139

ВятГУ 559

ГГДСК 171

ГомГМК 501

ГГМУ 1966

ГГТУ им. Сухого 4467

ГГУ им. Скорины 1590

ГМА им. Макарова 299

ДГПУ 159

ДальГАУ 279

ДВГГУ 134

ДВГМУ 408

ДВГТУ 936

ДВГУПС 305

ДВФУ 949

ДонГТУ 498

ДИТМ МНТУ 109

ИвГМА 488

ИГХТУ 131

ИжГТУ 145

КемГППК 171

КемГУ 508

КГМТУ 270

КировАТ 147

КГКСЭП 407

КГТА им. Дегтярева 174

КнАГТУ 2910

КрасГАУ 345

КрасГМУ 629

КГПУ им. Астафьева 133

КГТУ (СФУ) 567

КГТЭИ (СФУ) 112

КПК №2 177

КубГТУ 138

КубГУ 109

КузГПА 182

КузГТУ 789

МГТУ им. Носова 369

МГЭУ им. Сахарова 232

МГЭК 249

МГПУ 165

МАИ 144

МАДИ 151

МГИУ 1179

МГОУ 121

МГСУ 331

МГУ 273

МГУКИ 101

МГУПИ 225

МГУПС (МИИТ) 637

МГУТУ 122

МТУСИ 179

ХАИ 656

ТПУ 455

НИУ МЭИ 640

НМСУ «Горный» 1701

ХПИ 1534

НТУУ «КПИ» 213

НУК им. Макарова 543

НВ 1001

НГАВТ 362

НГАУ 411

НГАСУ 817

НГМУ 665

НГПУ 214

НГТУ 4610

НГУ 1993

НГУЭУ 499

НИИ 201

ОмГТУ 302

ОмГУПС 230

СПбПК №4 115

ПГУПС 2489

ПГПУ им. Короленко 296

ПНТУ им. Кондратюка 120

РАНХиГС 190

РОАТ МИИТ 608

РТА 245

РГГМУ 117

РГПУ им. Герцена 123

РГППУ 142

РГСУ 162

«МАТИ» — РГТУ 121

РГУНиГ 260

РЭУ им. Плеханова 123

РГАТУ им. Соловьёва 219

РязГМУ 125

РГРТУ 666

СамГТУ 131

СПбГАСУ 315

ИНЖЭКОН 328

СПбГИПСР 136

СПбГЛТУ им. Кирова 227

СПбГМТУ 143

СПбГПМУ 146

СПбГПУ 1599

СПбГТИ (ТУ) 293

СПбГТУРП 236

СПбГУ 578

ГУАП 524

СПбГУНиПТ 291

СПбГУПТД 438

СПбГУСЭ 226

СПбГУТ 194

СПГУТД 151

СПбГУЭФ 145

СПбГЭТУ «ЛЭТИ» 379

ПИМаш 247

НИУ ИТМО 531

СГТУ им. Гагарина 114

СахГУ 278

СЗТУ 484

СибАГС 249

СибГАУ 462

СибГИУ 1654

СибГТУ 946

СГУПС 1473

СибГУТИ 2083

СибУПК 377

СФУ 2424

СНАУ 567

СумГУ 768

ТРТУ 149

ТОГУ 551

ТГЭУ 325

ТГУ (Томск) 276

ТГПУ 181

ТулГУ 553

УкрГАЖТ 234

УлГТУ 536

УИПКПРО 123

УрГПУ 195

УГТУ-УПИ 758

УГНТУ 570

УГТУ 134

ХГАЭП 138

ХГАФК 110

ХНАГХ 407

ХНУВД 512

ХНУ им. Каразина 305

ХНУРЭ 325

ХНЭУ 495

ЦПУ 157

ЧитГУ 220

ЮУрГУ 309

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

3. Колебания и адиабатические инварианты

Законы колебательного движения обладают универсальностью, общностью для колебаний различной физической природы. Академик Л.И.Мандельштам отмечал: «Теория колебаний объединяет, обобщает различные области физики. Каждая из областей физики _ оптика, механика, акустика _ говорит на своем «национальном» языке. Но есть «интернациональный» язык, и это _ язык теории колебаний. Изучая одну область, вы получите тем самым интуицию и знания совсем в другой области».

Изменение параметров физической системы всегда сопровождается изменением некоторых характеристик ее движения. Однако в некоторых случаях в физической системе существуют характеристики, которые сохраняются при медленном (адиабатическом) изменении со временем каких-либо параметров системы. Такие величины называются адиабатическими инвариантами. Геометрический смысл инварианта- это площадь замкнутой фазовой траектории.

3.1 Гармонический осциллятор

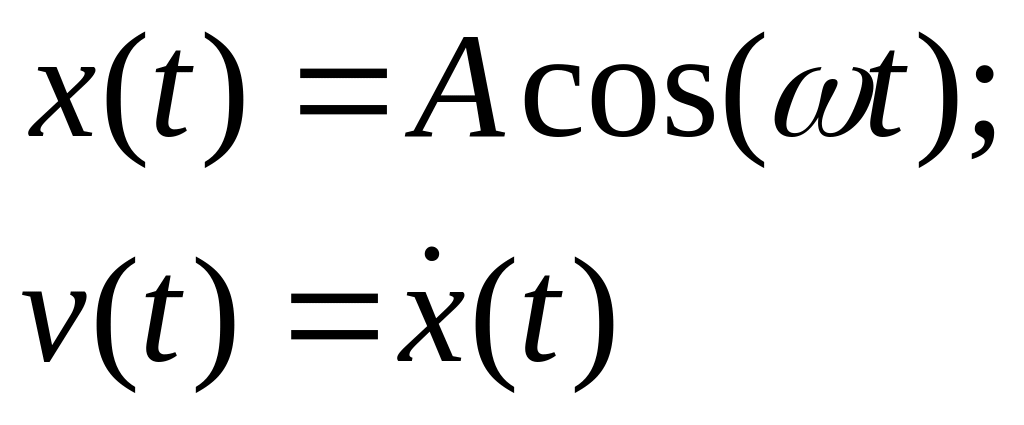
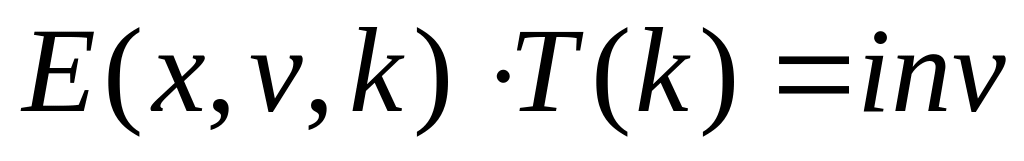
Из кинематики гармонических колебаний после несложных преобразований следует, что траектория осциллятора в фазовой плоскости (x,v) является эллипсом, размер которого определяется начальными условиями, а площадь его, равная произведению энергии на период является адиабатическим инвариантом ( ).

Рис.19. Адиабатический инвариант в трехмерной графике

Указание. Исследовать гамильтониан и фазовые траектории пружинного маятника при малых изменениях его жесткости, используя интерактивную компьютерную графику.

Слайд 16. Анимация гармонических колебаний

3.2 Задача «Бездонный колодец»

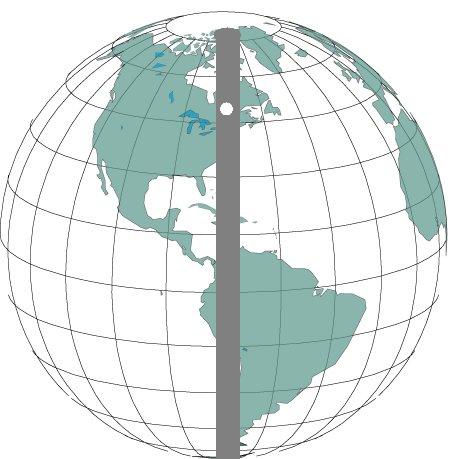
Предположим, что Земля просверлена по диаметру (рис.20). В образовавшийся колодец опустили небольшой предмет массой m. Определить характер движения тела и скорость в центре Земли без учета сопротивления воздуха. Масса Земли Мз=6 10 24 кг, радиус R= 6400 км.

Рис.20 . К задаче «Бездонный колодец»

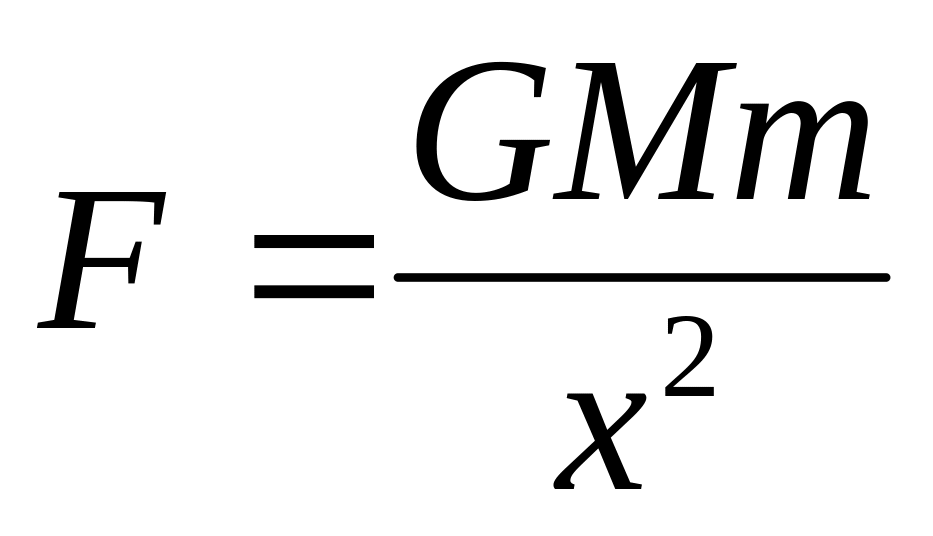
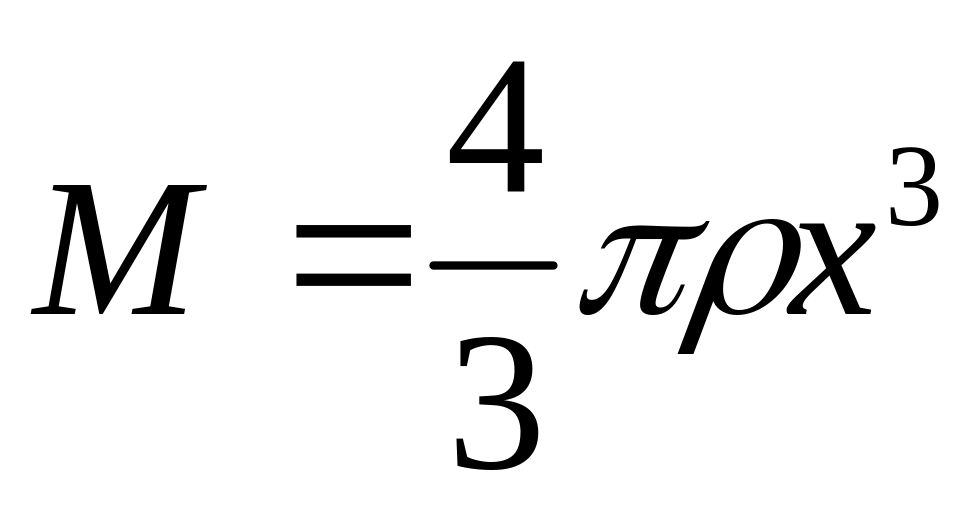
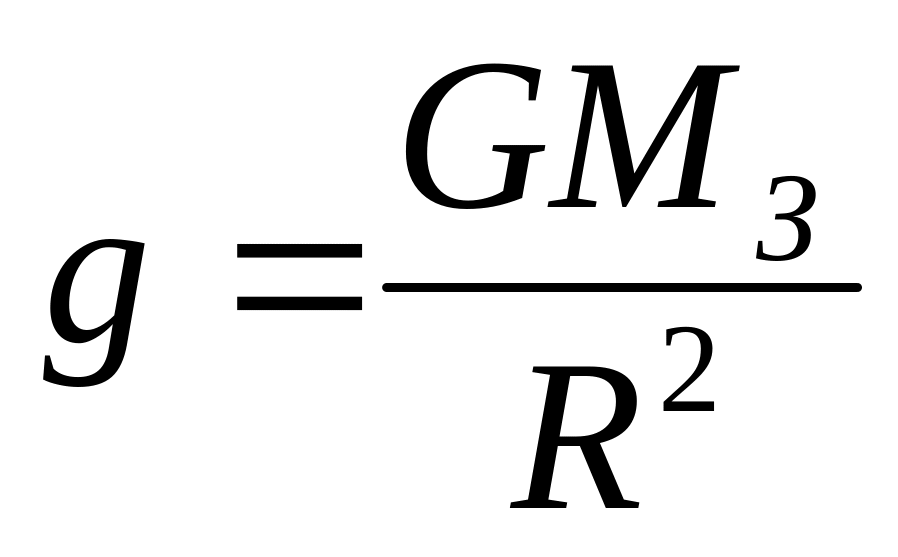
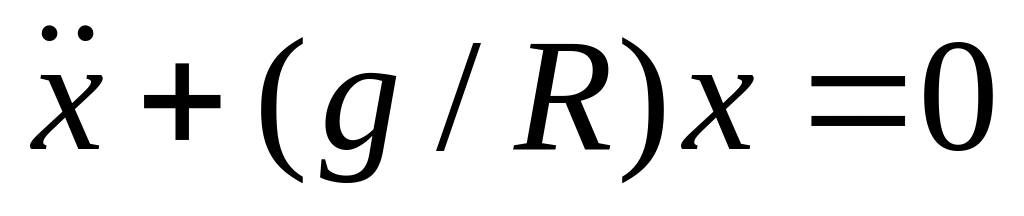
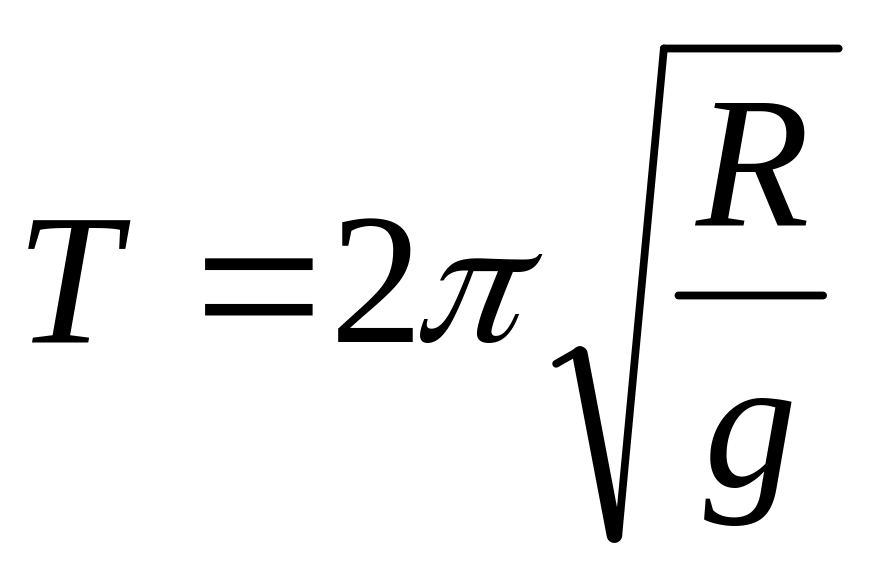
Взаимодействие с внешним шаровым слоем отсутствует, т.к. его можно разбить на сферы, внутри которых тяготения нет (задача Ньютона). Поэтому тело взаимодействует только с шаром радиуса «х» с силой , где масса шара- , плотность Земли (ось ОХ направлена по диаметру). Считая ускорение свободного падения на поверхности Земли и пренебрегая сопротивлением воздуха, после несложных преобразований находим дифференциальное уравнение движения , т.е. уравнение гармонических колебаний с периодом [4].

Вращение представляет собой суперпозицию перпендикулярных гармонических колебаний, поэтому полученное решение совпадает с периодом кругового вращения спутника (

1,5 час), а скорость в центре Земли совпадает с первой космической скоростью (

Указание. Рассмотреть проект «Сказочная дорога». Изучить движение тела в тоннеле, соединяющем две противоположные точки на поверхности Земли.

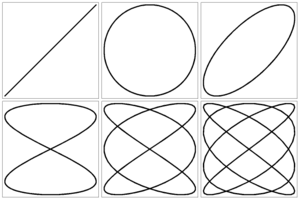
3.3 Фигуры Лиссажу

Демонстрация на экране монитора сложения двух взаимно перпендикулярных колебаний с различными амплитудами, частотами и разностями фаз (рис. 21)

Рис. 21. Сложение колебаний в плоскости

Слайд 17. Фигуры Лиссажу в анимационной графике

Источник

Читайте также: Человек с земли в хорошем качестве hd 1080