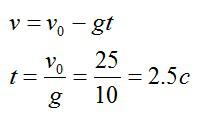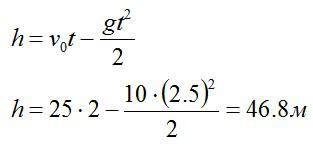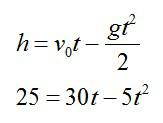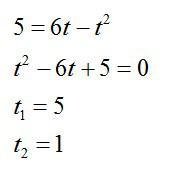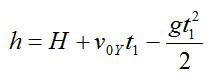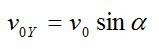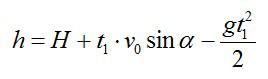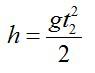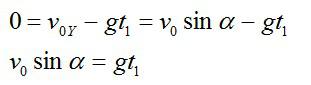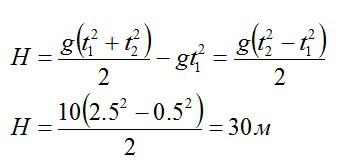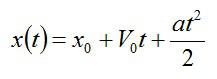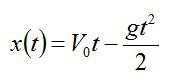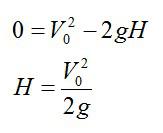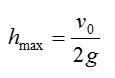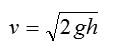Задачи на свободное падение тел: примеры решения задач по кинематике
Вторник, а это значит, что сегодня мы снова решаем задачи. На это раз, на тему «свободное падение тел».
Присоединяйтесь к нам в телеграм и получайте актуальную рассылку каждый день!
Задачи на свободное падение тел с решением
Задача №1. Нахождение скорости при свободном падении
Тело падает с высоты 20 метров. Какую скорость оно разовьет перед столкновением с Землей?
Высота нам известна по условию. Для решения применим формулу для скорости тела в момент падения и вычислим:
Ответ: примерно 20 метров в секунду.
Задача №2. Нахождение высоты и времени движения тела, брошенного вертикально.
Индеец выпускает стрелу из лука вертикально вверх с начальной скоростью 25 метров в секунду. За какое время стрела окажется в наивысшей точке и какой максимальной высоты она достигнет стрела?
Сначала запишем формулу из кинематики для скорости. Как известно, в наивысшей точке траектории скорость стрелы равна нулю:
Теперь запишем закон движения для вертикальной оси, направленной вертикально вверх.
Ответ: 2,5 секунды, 46 метров.
Задача №3. Нахождение времени движения тела, брошенного вертикально вверх
Мячик бросили вертикально вверх с начальной скоростью 30 метров в секунду. Через какое время мяч окажется на высоте 25 метров?
Запишем уравнение для движения мячика:
Мы получили квадратное уравнение. Упростим его и найдем корни:
Как видим, уравнение имеет два решения. Первый раз мячик побывал на высоте через 1 секунду (когда поднимался), а второй раз через 5 секунд (когда падал обратно).
Ответ: 1с, 5с.
Задача №4. Нахождение высоты при движении тела под углом к горизонту
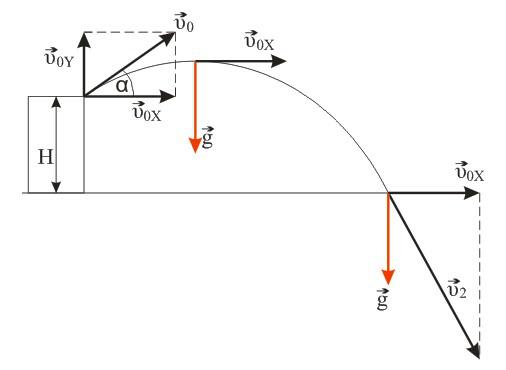
Камень, брошенный с крыши дома под углом альфа к горизонту, через время t1=0,5c достиг максимальной высоты, а еще через время t2=2,5c упал на землю. Определите высоту Н дома. Сопротивлением воздуха пренебречь. Ускорение свободного падения g = 10 м/с2.
Камень брошен со скоростью v0 под углом α к горизонту с дома высотой Н. Эту скорость можно разложить на две составляющие: v0X (горизонтальная) и v0Y (вертикальная). В горизонтальном направлении на камень не действует никаких сил (сопротивлением воздуха пренебрегаем), поэтому горизонтальная составляющая скорости неизменна на протяжении всего времени полета камня (равномерное движение). Максимальная точка траектории камня над уровнем земли (исходя из кинематических соотношений):
Здесь t1 – время подъема камня с высоты Н на высоту h; g – ускорение свободного падения.
Вертикальную составляющую скорости можно вычислить исходя из геометрических соображений:
Подставив выражение для скорости в первое уравнение, получим:
Также высоту h можно выразить через время t2 падения камня с высоты h на землю (исходя из кинематических соотношений и учитывая, что с вертикальная составляющая скорости в наивысшей точке равна нулю):
Для высоты дома можно записать:
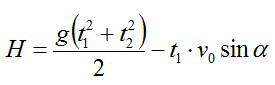
Так как вертикальная составляющая скорости камня в максимальной точке траектории равна нулю:
Подставляем в формулу для высоты H и вычисляем:
Ответ: H = 30 м.
Задача №5. Нахождение закона движения тела
Найти закон движения тела против силы тяжести, при начальной скорости V0. И на какую максимальную высоту поднимется тело? Тело бросили под углом 90 градусов.
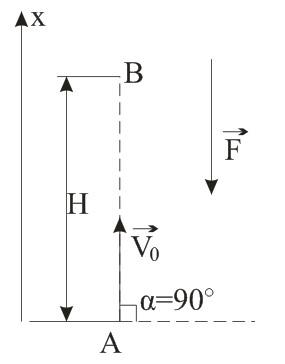
Тело брошено под углом α=90° к горизонту. Другими словами, тело брошено вертикально вверх с начальной скоростью V0. Направим координатную ось х вертикально вверх, так ее направление совпадает с вектором начальной скорости. F – сила тяжести, направленная вниз. В начальный момент тело находится в точке А.
В задаче нужно найти закон движения тела, то есть зависимость координаты тела от времени. В общем случае этот закон задается кинематическим соотношением:
где х0 – начальная координата тела; a – ускорение.
Так как мы поместили начало координат в точку А, х0=0. Тело движется с ускорением свободного падения g, при этом сила тяжести направлена против начальной скорости, поэтому в проекции на вертикальную ось a=-g. Таким образом, искомый закон движения перепишется в виде:
Далее будем использовать еще одно общее кинематическое соотношение:
Максимальная высота подъема тела указана на рисунке точной B, в этот момент конечная скорость V равна нулю, а координата х равна максимальной высоте Н подъема тела. Отсюда можно найти выражение для этой величины:
Полезные формулы для решения задач на свободное падение
Свободное падение описывается формулами кинематики. Мы не будем приводить их вывод, но запишем самые полезные.
Формула для максимальной высоты подъема тела, брошенного вертикально вверх c некоторой начальной скоростью:
Кстати, как выводится именно эта формула можно посмотреть в последней задаче.
Формула для времени подъема и падения тела, брошенного вертикально вверх:
Скорость тела в момент падения с высоты h:
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Вопросы с ответами на свободное падение тел
Вопрос 1. Как направлен вектор ускорения свободного падения?
Ответ: можно просто сказать, что ускорение g направлено вниз. На самом деле, если говорить точнее, ускорение свободного падения направлено к центру Земли.
Вопрос 2. От чего зависит ускорение свободного падения?
Ответ: на Земле ускорение свободного падения зависит от географической широты, а также от высоты h подъема тела над поверхностью. На других планетах эта величина зависит от массы M и радиус R небесного тела. Общая формула для ускорения свободного падения:
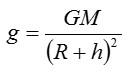
Вопрос 3. Тело бросают вертикально вверх. Как можно охарактеризовать это движение?
Ответ: В этом случае тело движется равноускоренно. Причем время подъема и время падения тела с максимальной высоты равны.
Вопрос 4. А если тело бросают не вверх, а горизонтально или под углом к горизонту. Какое это движение?
Ответ: можно сказать, что это тоже свободное падение. В данном случае движение нужно рассматривать относительно двух осей: вертикальной и горизонтальной. Относительно горизонтальной оси тело движется равномерно, а относительно вертикальной – равноускоренно с ускорением g.
Баллистика – наука, изучающая особенности и законы движения тел, брошенных под углом к горизонту.
Вопрос 5. Что значит «свободное» падение.
Ответ: в данном контексте понимается, что тело при падении свободно от сопротивления воздуха.
Свободное падение тел: определения, примеры
Свободное падение – равноускоренное движение, происходящее под действием силы тяжести.
Первые попытки систематизированно и количественно описать свободное падение тел относятся к средневековью. Правда, тогда было широко распространено заблуждение, что тела разной массы падают с разной скоростью. На самом деле, в этом есть доля правды, ведь в реальном мире на скорость падения сильно влияет сопротивление воздуха.
Однако, если им можно пренебречь, то скорость падающих тел разной массы будет одинакова. Кстати, скорость при свободном падении возрастает пропорционально времени падения.
Ускорение свободно падающих тел не зависит от их массы.
Примеры свободного падения тел:
- яблоко летит на голову Ньютона;
- парашютист выпрыгивает из самолета;
- перышко падает в герметичной трубке, из которой откачан воздух.
При свободном падении тела возникает состояние невесомости. Например, в таком же состоянии находятся предметы на космической станции, движущейся по орбите вокруг Земли. Можно сказать, что станция медленно, очень медленно падает на планету.
Конечно, свободное падение возможно не только не Земле, но и вблизи любого тела, обладающего достаточной массой. На других комических телах падения также будет равноускоренным, но величина ускорения свободного падения будет отличаться от земной. Кстати, раньше у нас уже выходил материал про гравитацию.
При решении задач ускорение g принято считать равным 9,81 м/с^2. В реальности его величина варьируется от 9,832 (на полюсах) до 9,78 (на экваторе). Такая разница обусловлена вращением Земли вокруг своей оси.
Нужна помощь в решении задач по физике? Обращайтесь в профессиональный студенческий сервис в любое время.
Источник
Тело брошено вертикально вверх с поверхности земли в момент времени
Источник задания: Решение 4040. ЕГЭ 2017. Физика. Демидова М. Ю. 30 вариантов.
Задание 5. На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Выберите два утверждения, которые соответствуют результатам опыта.
1) В процессе наблюдения кинетическая энергия тела все время увеличивалась.
2) В конце наблюдения кинетическая энергия тела становится равной нулю.
3) Тело брошено под углом к горизонту с балкона и упало на землю.
4) Тело брошено под углом к горизонту с поверхности земли и упало обратно на землю.
5) Тело брошено вертикально вверх с балкона и упало на землю.
1) Из графика видно, что кинетическая энергия сначала убывает, а затем, увеличивается.
2) В конце наблюдения (после пунктирной линии) кинетическая энергия резко становится равной нулю.
3) При бросании тела под углом к горизонту начальная скорость тела v раскладывается на вертикальную и горизонтальную составляющие, причем, в горизонтальной плоскости тело совершает равномерное движение, а в вертикальной плоскости скорость тела постепенно уменьшается на величину ускорения свободного падения. Когда вертикальная скорость тела станет равна 0, тело достигает наибольшей высоты, а кинетическая энергия своего минимального значения. Обратите внимание, что при этом кинетическая энергия, равная 
, не будет равна нулю, так как горизонтальная составляющая скорости тела отлична от нуля. При падении вертикальная скорость тела начинает постепенно увеличиваться, на уровне балкона сравнивается с начальной скоростью, а затем, увеличиваясь, достигает земли, где скорость резко обнуляется. Это означает, что кинетическая энергия увеличиваясь, достигает своего первоначального значения, превышает его, а затем, резко становится равной нулю. Все это соответствует графику на рисунке.
4) Если бы тело было брошено с земли, то максимальная кинетическая энергия была бы равна первоначальному значению (при t=0).
5) Если бы тело было брошено вертикально вверх, то в точке максимального подъема кинетическая энергия была бы равна нулю, однако на графике она не обращается в ноль.
Источник
Тело брошено вертикально вверх с поверхности земли в момент времени
На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени.
Выберите два верных утверждения, описывающих движение в соответствии с данным графиком.
1) В конце наблюдения кинетическая энергия тела отлична от нуля.
2) Кинетическая энергия тела в течение всего времени наблюдения уменьшается.
3) Тело брошено под углом к горизонту и упало на балкон.
4) Тело брошено вертикально вверх с балкона и упало на Землю.
5) Тело брошено под углом к горизонту с поверхности Земли и упало в кузов проезжающего мимо грузовика.
Проверим справедливость предложенных утверждений.
1) Из графика видно, что в конце наблюдения кинетическая энергия тела больше нуля.
2) Кинетическая энергия тела в течение наблюдения сначала падает, затем возрастает, после вновь падает.
3) Если бы тело было брошено под углом к горизонту и затем упало на балкон, то конечная кинетическая энергия тела была бы равна нулю, в данном случае это не так.
4) Если бы тело было брошено вертикально вверх с балкона и упало на Землю, то конечная кинетическая тела энергия была бы равна нулю, в данном случае это не так.
5) Если бы тело было брошено под углом к горизонту с поверхности Земли и упало в кузов проезжающего мимо грузовика, то изменение кинетической энергии тела было бы таким, как представлено на графике.
Таким образом, верными являются утверждения под номерами 1 и 5.
На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени.
Выберите два верных утверждения, описывающих движение в соответствии с данным графиком.
1) В процессе наблюдения кинетическая энергия тела все время увеличивалась.
2) В конце наблюдения кинетическая энергия тела становится равной нулю.
3) Тело брошено под углом к горизонту с балкона и упало на землю.
4) Тело брошено под углом к горизонту с поверхности земли и упало обратно на землю.
5) Тело брошено вертикально вверх с балкона и упало на землю.
Проверим справедливость предложенных утверждений.
1) Кинетическая энергия тела в течение наблюдения сначала падает, затем возрастает, после вновь падает.
2) Из графика видно, что в конце наблюдения кинетическая энергия тела равна нулю.
3) Если бы тело было брошено под углом к горизонту и затем упало на землю, то изменение кинетической энергии тела было бы таким, как представлено на графике.
4) Если бы тело было брошено под углом к горизонту с поверхности земли и упало на землю, то конечная кинетическая тела энергия не могла бы превышать начальную кинетическую энергию тела, в данном случае конечная кинетическая энергия тела превышает начальную.
5) Если бы тело было брошено вертикально вверх, то его кинетическая энергия в верхней точке обращалась бы в ноль, это не так.
Таким образом, верными являются утверждения под номерами 2 и 3.
ответ верен, не верно 5 пояснение. если бросить вертикально вверх, в верхней точке кинетическая энергия будет равна 0, что из графика не видно.
В пятом случае относительно поверхности земли кинетическая энергия тела была бы ненулевой.
Утверждение 2 не верно, в конце кин. энергия максимальна.
В середине седьмой клеточки времени кинетическая энергия резко уменьшается до нуля и остаётся нулевой до конца эксперимента.
Бусинка может свободно скользить по неподвижной горизонтальной спице. На графике изображена зависимость ее координаты от времени. Выберите два утверждения, которые можно сделать на основании графика.
1) Скорость бусинки на участке 1 постоянна, а на участке 2 равна нулю.
2) Проекция ускорения бусинки на участке 1 положительна, а на участке 2 — отрицательна.
3) Участок 1 соответствует равномерному движению бусинки, а на участке 2 бусинка неподвижна.
4) Участок 1 соответствует равноускоренному движению бусинки, а участок 2 — равномерному.
5) Проекция ускорения бусинки на участке 1 отрицательна, а на участке 2 — положительна.
Проверим справедливость предложенных утверждений.
1) Скорость — тангенс угла наклона графика зависимости координаты от времени. Из графика видно, что скорость на первом участке не равна нулю и постоянна, а на участке 2 равна нулю.
2) Скорость на первом и втором участках постоянна, поэтому ускорение на обоих участках равно нулю.
3) На первом участке скорость бусинки постоянна, на втором участке координата бусинки не меняется со временем, бусинка не подвижна.
4) Скорость на первом и втором участках постоянна, поэтому ускорение на обоих участках равно нулю. Следовательно, на первом участке бусинка движется равномерно, а на втором — неподвижна.
5) Скорость на первом и втором участках постоянна, поэтому ускорение на обоих участках равно нулю.
Таким образом, верными являются утверждения под номерами 1 и 3.
Шарик катится по желобу. Изменение координаты шарика с течением времени в инерциальной системе отсчета показано на графике. Выберите два утверждения, которые соответствуют результатам опыта.
1) Проекция скорости шарика постоянно увеличивалась и оставалась отрицательной на всем пути.
2) Первые 2 с скорость шарика возрастала, а затем оставалась постоянной.
3) Первые 2 с шарик двигался с уменьшающейся скоростью, а затем покоился.
4) На шарик действовала все увеличивающаяся сила.
5) Первые 2 с проекция ускорения шарика не изменялась, а затем стала равной нулю.
Проверим справедливость предложенных утверждений.
Скорость — тангенс угла наклона графика зависимости координаты от времени. Из графика видно, что тангенс угла наклона графика в первые две секунды положителен, а затем равен нулю, то есть скорость шарика постоянно уменьшалась и была неотрицательной на протяжении всего пути. Первые две секунды шарик двигался с уменьшающейся скоростью, а затем остановился. Первые две секунды шарик двигался с ускорением, направленным в сторону, противоположную оси x, а после ускорение шарика стало равным нулю. Значит, первые две секунды на шарик действовала сила, затем величина этой силы стала равной нулю.
Таким образом, верными являются утверждения под номерами 3 и 5.
Источник